import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
np.random.seed(1)
k-means clustering¶
k-means clustering is an algorithm that searches for a given number of clusters within some unlabeled multidimensional dataset. The optimal clustering is found as follow:
The “cluster centre” is the arithmetic mean of all of the points belonging to the cluster.
Each point is closer to its own cluster centre than other cluster centres.
These assumptions are the basis for the k-means algorithm, which is implemented with an expectation-maximisation (E-M) approach. The E-M approach consists of the following procedure:
Guess some cluster centres
Repeat the following to convergence:
E-step: assign points to the nearest cluster centre
M-step: set the cluster centres to the mean
The E-step updates our expectation of which cluster each point belongs to, while the M-step maximises some fitness function that defines the cluster centre locations. In the case of k-means, the maximisation is achieved by taking a simple mean of the data in each cluster. Each repatition will always result in a better estimate of the cluster characteristics.
The k-means algorithm is simple enough that it can be written with just a few handfulls of lines of code, see the example below from the work of VanderPlas [Van16].
def find_clusters(X, n_clusters):
# 1. Guess some cluster centres
i = np.random.permutation(X.shape[0])[:n_clusters]
centres = X[i]
while True:
# 2A. Assign points to the nearest cluster centre
labels = pairwise_distances_argmin(X, centres)
# 2B. Set the cluster centres to the mean
new_centres = np.array([X[labels == i].mean(axis=0) for i in range(n_clusters)])
# Check convergence
if np.all(centres == new_centres):
break
centres = new_centres
return centres, labels
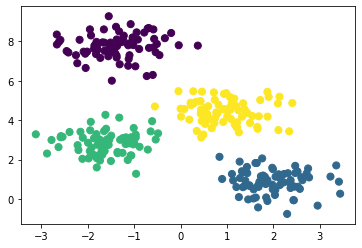
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=0)
centres, labels = find_clusters(X, 4)
plt.scatter(X[:, 0], X[:, 1], s=50, c=labels)
plt.show()
There are some important issues that we need to be aware of when using a simple E-M algorithm:
The globally optimal result may not be achieved: As is the case with all optimisations, although the result is improving, it may not be moving towards to global optimium solution.
The number of clusters must be selected beforehand: It is necessary that we have some a priori knowledge about our dataset to effectively apply a k-means clustering, as we must now at the beginning how many clusters we expect to find.
k-means is limited to linear cluster boundaries: The fact that k-means is finding samples as close as possible in cartesian space means that the clusters cannot have more complex geometries.
k-means can be slow for large numbers of samples: Each iteration must access every point in the dataset, this means that this algorithm can be slow for very large datasets.
Let’s quickly see the how to leverage the k-means algorithm in scikit-learn before we move on to a more complex method.
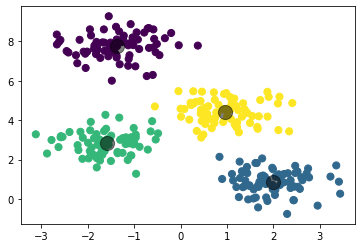
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_means = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], s=50, c=labels)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='k', alpha=0.5)
plt.show()